|
|
自己写的numpy BP神经网络(拟合[0,2]上的函数 sin(2 pi x)/4+0.5 )第一次跑通,兴奋之余胡乱修改了网络结构。看着loss曲线时而下降,时而振荡,突然,有一个网络(代码附在文末)啥也没学到,但给出了熟悉的图案:
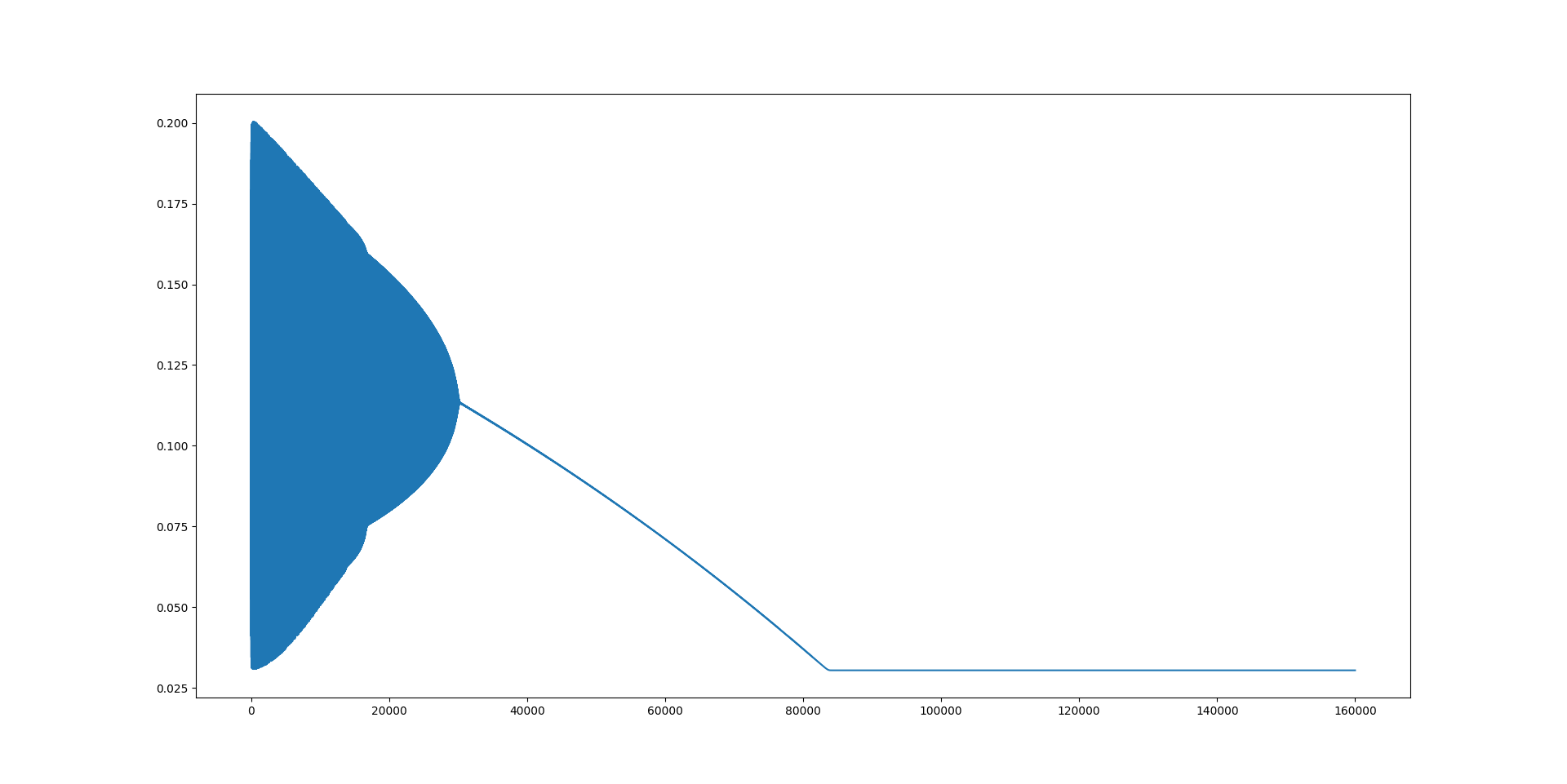
赶紧把loss曲线的数据小心翼翼的导出来,作散点图,果不其然:
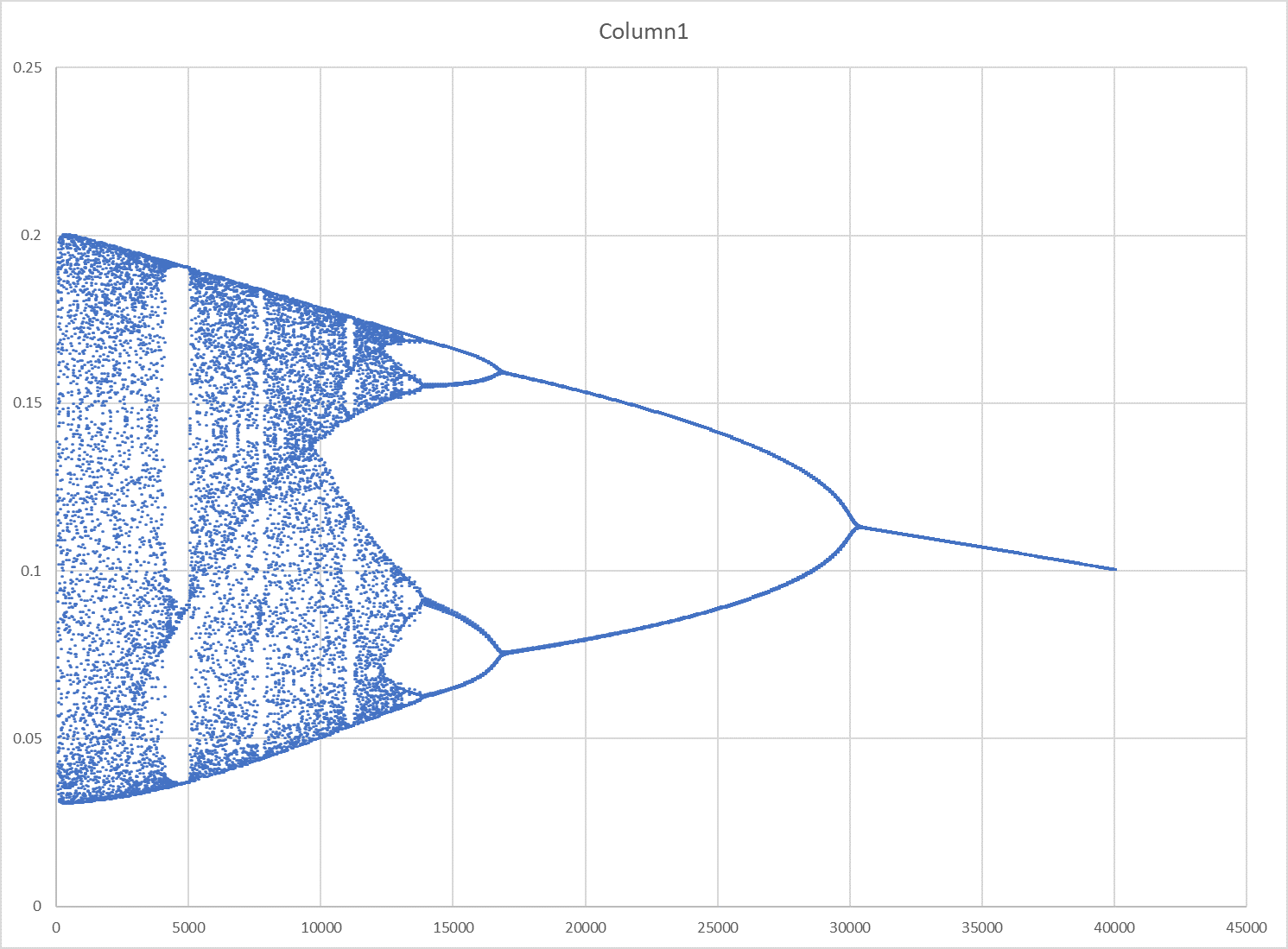
原来训练集为间隔0.1采样,反复试验均无分岔图案;当训练集改为间隔0.05采样时,出现了分岔图案。
反复运行了好几次,都能出现这种图样,说明与参数初始化无关。
抽去了一个2节点/sigmoid激活函数的层,仍然出现了类似的分岔图(代码是抽去之后的)。
没有照抄大佬的代码,以下代码说不定有错;但经过试验,取间隔0.1采样的数据集,很小的网络规模(1,3,3,1,全sigmoid),还是能看出它在试图拟合一个函数的。
<hr/>第一次更新:
补充一些实验结果:
@Horizony 大佬和 @镇戎 大佬所言甚妙:将待拟合的函数换成常函数y=0.5,仍然出现相同的图样。
分岔的发生与采样点的密度有关;而分岔“合并”的速率与学习率的衰减有关:学习率衰减越快,分岔合并得也越快。不负责任地推测,假设那儿已经有了一张完整的分岔图,而加密采样点起“平移”作用,加快/减慢学习率衰减起伸/缩作用。
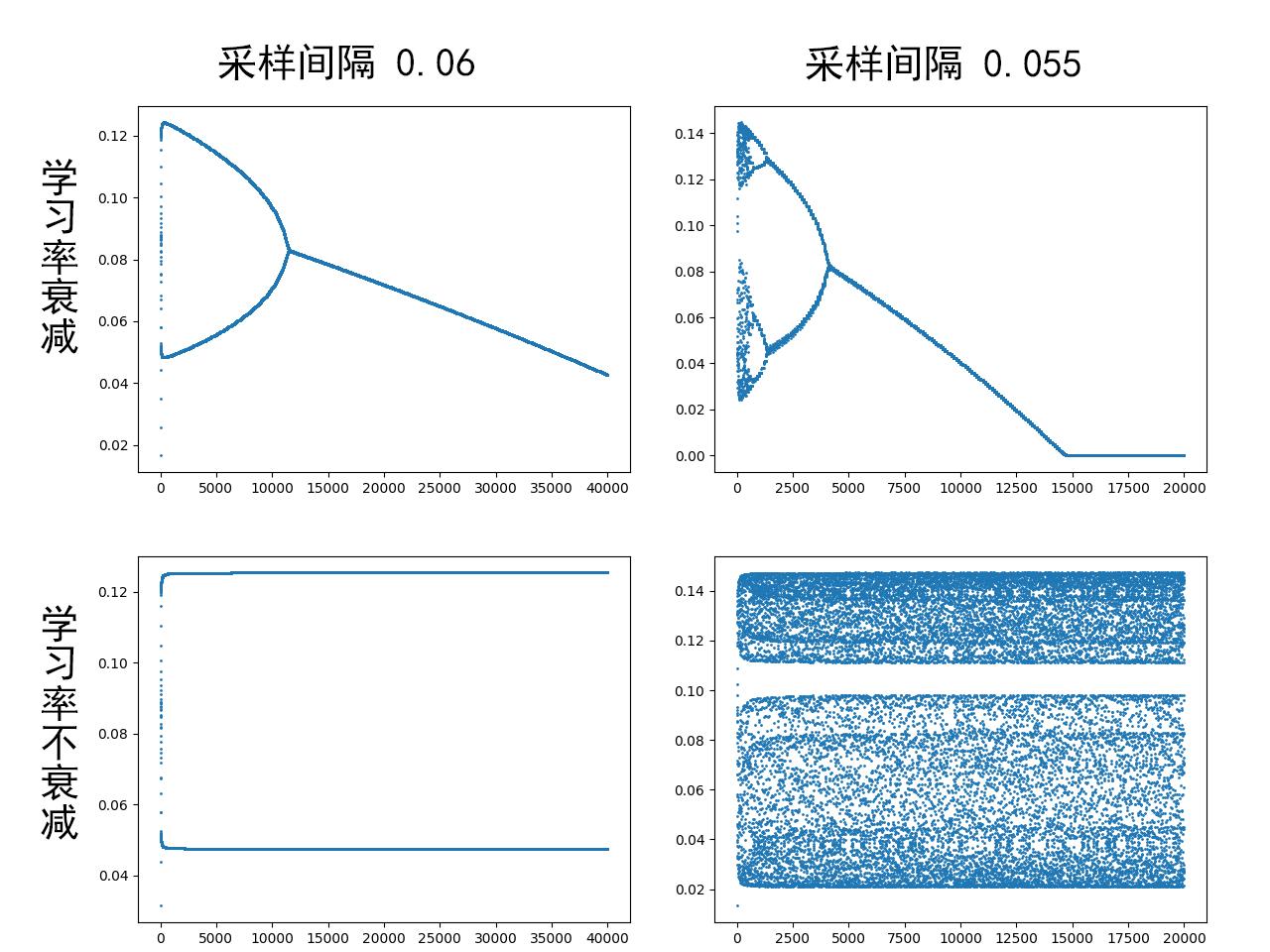
注意到上图的散点图出现了一些台阶的特征,这是不必要的设置——每100次迭代衰减一次学习率造成的。去除这个设置后,散点图显得更平滑(相应地可以将迭代次数减少到百分之一)。
混沌很可能是sigmoid激活函数导致的,而relu不起作用:单层,甚至单个sigmoid神经元足以产生分岔图样,虽然并不像Logistic。
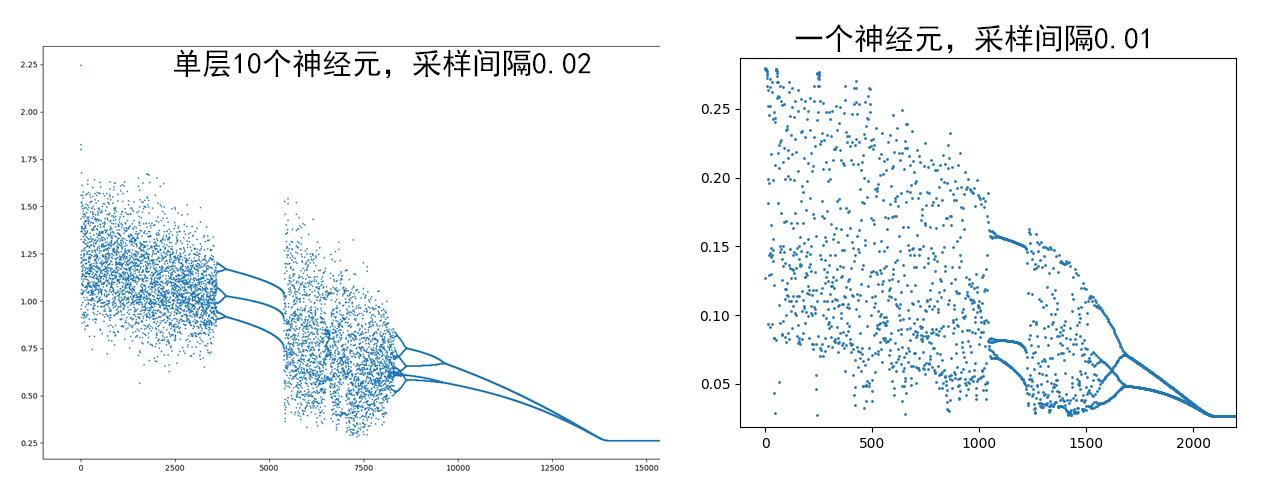
解析计算似乎有希望了?
目前为止,最令我惊讶的是,我本以为最无关的参数——采样间隔,反而是控制着分岔图样出现的最关键参数,实在匪夷所思。
会不会有这么一种可能:每个神经网络的loss曲线都是某个混沌映射的反向的图样,只是平时因为位置或伸缩不合适而看不出来?
2022/9/21
import numpy as np
import copy as cp
import matplotlib.pyplot as plt
def sig(x):
return 1 / (1 + np.exp(-x))
def dsig(x):
s = sig(x)
return np.exp(-x) * s * s
def relu(x):
if x < 0: return 0.1 * x
return x
def drelu(x):
if x >= 0: return 1
return 0.1
Sig = (sig, dsig)
Relu = (np.vectorize(relu), np.vectorize(drelu))
class ConnectLayer:
def __init__(self, inp, output, func_tup, lrate_tup):
self.inp = inp
self.output = output
self.func = func_tup[0]
self.dfunc = func_tup[1]
self.lrate = lrate_tup[0]
self.lrate_decay = lrate_tup[1]
self.decay_cnt = 0
self.w = np.random.random((output, inp))
self.b = np.random.random((output, 1))
self.yjs_cache = None
self.xjs_cache = None
def forward(self, xs):
# n = xs.shape[1]
self.xjs_cache = xs
yjs = self.w @ xs + self.b
self.yjs_cache = yjs
return self.func(yjs)
def backF(self, upstream): # f对y求导
return self.dfunc(self.yjs_cache) * upstream
def backPass(self, upstream): # y对x求导
return self.w.T @ upstream
def refw(self, upstream): # y对w求导
return upstream @ self.xjs_cache.T
def refb(self, upstream): # y对b求导
# 注意:不要直接使用np.sum,否则行列不稳定
db = np.sum(upstream, axis=1)
return db.reshape(self.b.shape)
def backward(self, upstream):
M = self.backF(upstream)
self.w -= self.lrate * self.refw(M)
self.b -= self.lrate * self.refb(M)
self.decay_cnt += 1
if self.decay_cnt == 100:
self.lrate *= self.lrate_decay
self.decay_cnt = 0
return self.backPass(M)
def g(x):
return np.sin(2 * np.pi * x) / 4 + 0.5
def genData():
xs = np.arange(0, 2.001, 0.05)
n = len(xs)
ys = []
for x in xs:
ys.append(g(x))
ys = np.array(ys)
return xs.reshape(1, n), ys.reshape(1, n)
def mse(fjs, yjs):
m, n = yjs.shape
delta = fjs - yjs
return np.sum(delta * delta) / m / n
def dmse(fjs, yjs):
return 2 * (fjs - yjs)
Mse = (mse, dmse)
class ScalarLayer:
def __init__(self, inp, answer, loss_tup):
self.inp = inp
self.answer = answer
self.loss = loss_tup[0]
self.dloss = loss_tup[1]
def forward(self, fyjs):
return self.loss(fyjs, self.answer)
def backward(self, fyjs): # L对f求导
return self.dloss(fyjs, self.answer)
class nn:
def __init__(self, layer_msg, funcs_msg, loss, xs, ys, lrate):
self.layer_msg = layer_msg
self.layers = []
self.xs = xs
self.ys = ys
for i in range(len(layers_msg) - 1):
self.layers.append(ConnectLayer(
inp=layers_msg,
output=layers_msg[i + 1],
func_tup=funcs_msg,
lrate_tup=lrate
))
self.outlet = ScalarLayer(1, ys, loss)
def train(self, TURNS):
ls = []
for t in range(TURNS):
# 单步训练
data = cp.deepcopy(self.xs)
for lay in self.layers:
data = lay.forward(data)
L = self.outlet.forward(data)
data = self.outlet.backward(data)
for lay in self.layers[::-1]:
data = lay.backward(data)
ls.append(L)
return ls
def test(self):
newxs = np.hstack((self.xs - 1, self.xs + 1))
data = cp.deepcopy(newxs)
for lay in self.layers:
data = lay.forward(data)
return newxs, data
if __name__ == &#39;__main__&#39;:
xs, ys = genData()
layers_msg = [1, 4, 2, 2, 1]
funcs_msg = [Relu, Sig, Sig, Sig]
model = nn(layers_msg, funcs_msg, Mse, xs, ys, lrate=(0.3, 0.999))
ls = model.train(40000)
plt.plot(ls)
plt.show()
print(&#39;end&#39;) |
|