|
|
如何补题 PTA | 程序设计类实验辅助教学平台 ,然后不要选择买时光机。

如果没有金币可以在上面的签到领取

C
题意:
给定一棵树,你可以执行以下操作。
(1)删除一个点
(2)删除一个度数为2的点,但是会把这个点连接的两个点用一条新边来连接
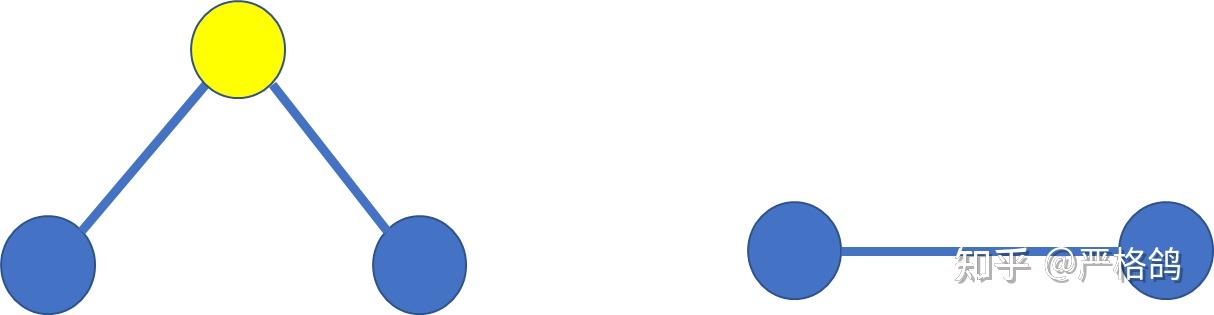
问把树的点都删除,最少需要多少个操作(1)
做法:
因为每个操作都只会删除一个点,所以我们有 (1) + (2) = n
还发现,当执行一个操作(2)后,会相连的两个点的度数不会发生改变。
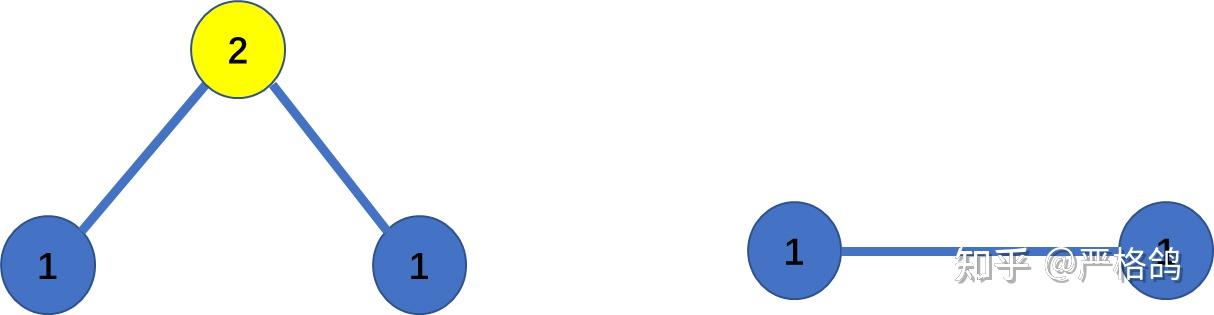
而度数为1的点,只能由操作(1)删除,并且会是的相连那个点的度数减一
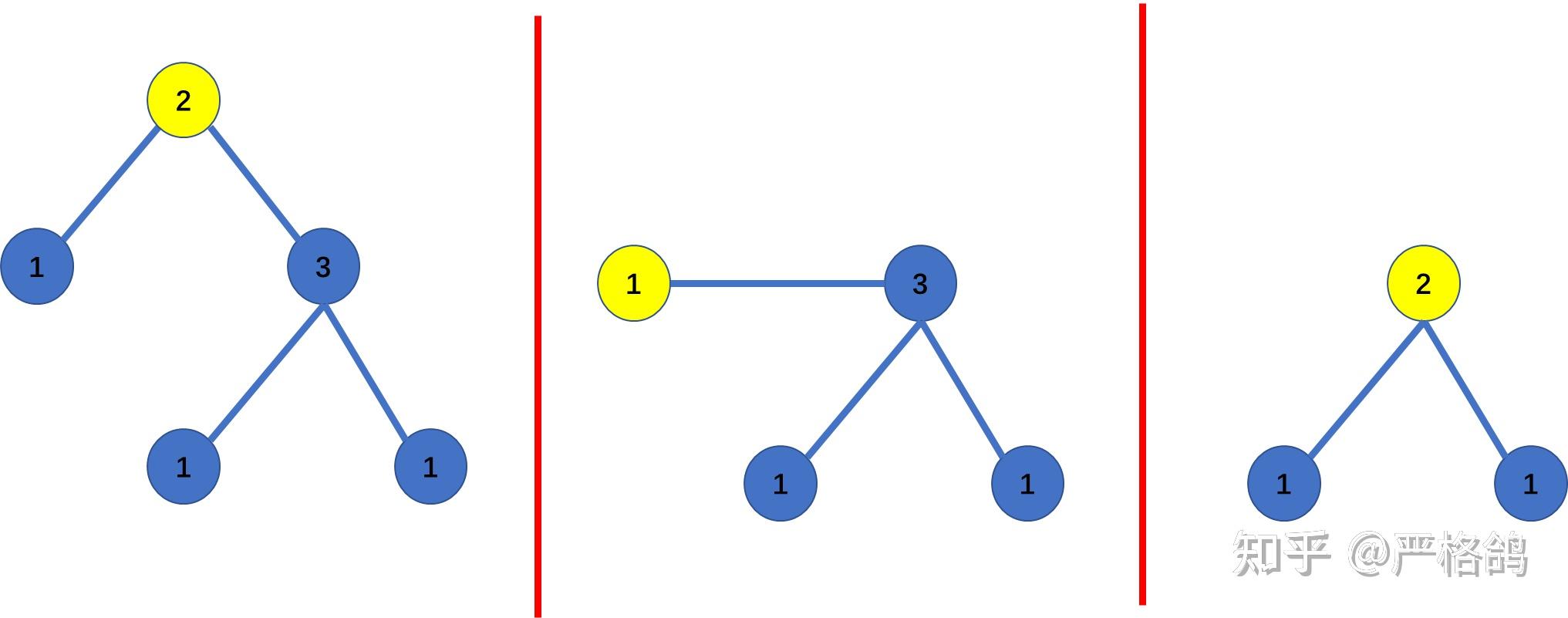
并且我们手玩样例发现,叶子节点的个数就是答案
H
题意:
有一个自己写的语言,由固定的语法。问library执行了多少次。
实际上,我们可以理解为对下面的字符串进行求值
(((1 + 1 + 1) * 3 )* 3 + 1 )*12
做法:
我们直接用栈来模拟既可,如果你不会的话,可以在力扣上搜索”计算器“
D
题意:
定义函数 ctz(x) 为x的二进制下后缀0的个数例如 ctz(1001000_2) = 3
pop(x) 为 x 的二进制下1的个数 pop(100101_2) = 3
定义一个数 x 是好数,需要满足 ctz(x) = pop(x) 。
现在给出 10^5 次询问,每次给出一个区间 [l,r](l,r \le 10^9) ,问这个区间中是否有一个好数。
做法:
比赛的时候打表发现,1e9范围内的好数只有5e5个,所以我们直接dfs暴力处理出所有的好数,最后排序二分搜索即可。
严格鸽:ICPC 网络赛 D 的几种枚举方式
A
题意:
给出一个01字符串组成的环。
你可以执行删除操作,选择一个1,删除这个数,及其左右两边的数。
例如
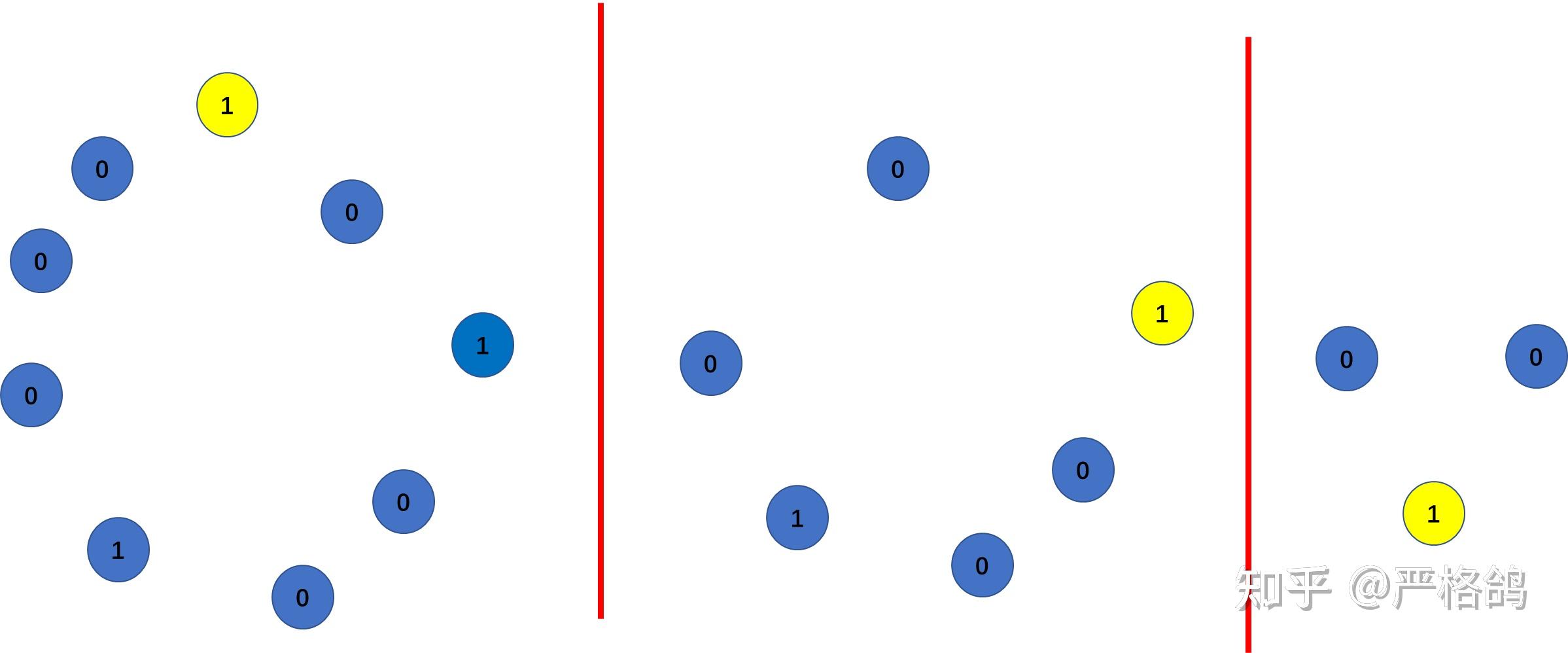
如果一个字符串可以被完全删除,则称这个字符串是个好字符串。
现在给出 10^6 次询问,每次询问给出一个区间 [l,r] 保证区间长度是3的倍数。
问 s[l...r] 是不是一个好字符串。
做法:
我们发现,如果长度为3的话,那么只要有一个1就可以完全删除。
如果长度为6的话。理论上两个1就可以完全删除
但是,以下情况不行

也就是两个1相邻。
但是只要两个1不相邻的话,我们就可以删除然后变成长度为3只有一个1的情况

那么我们看下长度为9的情况
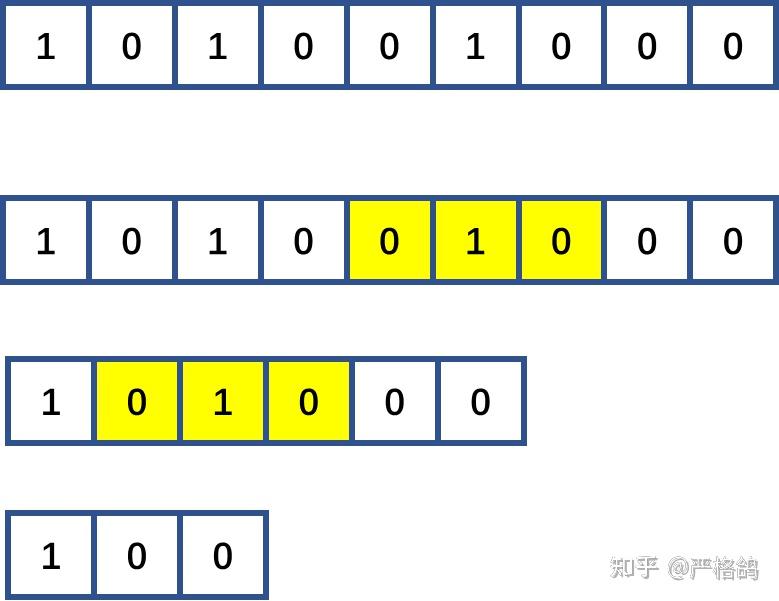
所以发现,只要字符串中,不相邻的1的个数大于等于区间长度 / 3的话,就可以完全删除了。
但是如果需要连续的1的呢?我们可以假装他是多个不相邻的1

那么对于一段区间,我们拆成几个部分。

即左右端点伸展的连续的1的个数,和中间的一段。
那么这个是可以预处理出来
(这里我们放上赛时的代码,为什么会保存赛时的代码呢?因为队友阿汤在调试的时候点错了,直接点提交了,然后在一阵卡顿后,AC了.....
code
void slove() {
cin >> n >> m;
string s; cin >> s;
s = "?" + s;
int cnt = 0;
for (int i = 1; i <= n; i++) {
if (s == &#39;1&#39;) cnt++;
else cnt = 0;
f = f[i - cnt - 1] + cnt / 2 + cnt % 2;
pre = cnt;
}
cnt = 0;
for (int i = n; i; i--) {
if (s == &#39;1&#39;) cnt++;
else cnt = 0;
last = cnt;
}
while (m--) {
int tmp = 0;
int l, r; cin >> l >> r;
tmp = pre[r] + last[l];
int st = f[r - pre[r]] - f[l + last[l]] + tmp / 2 + tmp % 2;
if ((r - l + 1) / 3 <= st) cout << 0 << endl;
else cout << (r - l + 1) / 3 - st << endl;
}
}
L
题意:
给定两个字符串 s,t(|s|,|t| \le 5*10^5)
你需要在 s 中找到一个最长的子序列 s&#39; ,满足 s&#39; 和 t 的任意一个公共子序列,长度都不超过1。
输出 s&#39; 的长度。
做法:
我们预先处理出一个ban的可能,如果 ban[a] = 1 ,则表明在选择的 s&#39; 中,不能出现 a....b 这样的
for (int i = m; i; i--) {
for (int j = 0; j < 26; j++)
if (vis[j]) ban[t][j] = 1;
vis[t] = 1;
}
然后我们定义, dp[j] 为选择 [1...i] 的子串构成的子序列,最后一个字符为 j 的最大长度。
考虑转移,如果 s 都没有在 t 中出现过,我们直接 dp[j] = dp[i - 1][j] + 1 。
你可能会奇怪,不是应该以 s 为结尾吗?但是因为 s 都没有在 t 中出现过,例如
s = aaeebb,t = ab ,这个e我们是可以随便选的。
(其实dp[j]的准确定义为[1...i]中最后一个为j(j在t中出现过)的最大长度) 然后我们枚举 s 放到某个 j 后面,我们需要保证 (j,s) 是没有被ban过的
for (int j = 0; j < 26; j++) {
if (!ban[j][s])
dp[s] = max(dp[s], dp[i - 1][j] + 1);
}
然后你可能又会奇怪,你只是保证了相邻的两个字符没有没ban,不会出现这种
(a,b)(b,c) 没有被ban (ban[a] = 0,ban[c] = 0
但是 (a,c) 被ban了( ban[a][c] = 1 )
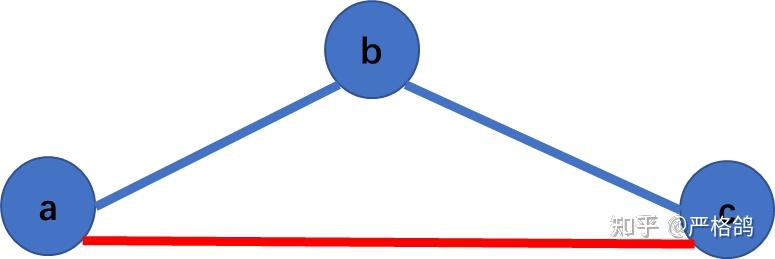
我们考虑下是否会有这种情况。
因为 (a,c) 被ban了,所以在t中 a 一定在 c 前面

我们考虑 b 的位置。
(b,c)被ban了

(a,b)(b,c)被ban了

(a,b)被ban了

也就是说,不会有这种情况,所以直接转移吧!
code
void slove() {
cin >> s + 1;
cin >> t + 1;
int n = strlen(s + 1), m = strlen(t + 1);
for (int i = 1; i <= n; i++)s -= &#39;a&#39;;
for (int i = 1; i <= m; i++)t -= &#39;a&#39;;
for (int i = m; i; i--) {
for (int j = 0; j < 26; j++)
if (vis[j]) ban[t][j] = 1;
vis[t] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 26; j++) {
dp[j] = dp[i - 1][j] + (vis[s] == 0);
}
if (vis[s] == 0)continue; //没有在t中出现的字符已经在上面转移完了
dp[s] = max(dp[s], 1);//初始化
for (int j = 0; j < 26; j++) {
if (!ban[j][s])
dp[s] = max(dp[s], dp[i - 1][j] + 1);
}
}
int ans = 0;
for (int i = 0; i < 26; i++)
ans = max(ans, dp[n]);
cout << ans << &#34;\n&#34;;
} |
|